The points F_c and B_c are common to both planes; for each plane, then, the parametric equation of the plane in form Ax + By + Cz = D is given by

where the components of (vector) n_F are equivalent to [A,B,C] for the plane containing F₁, F_c and B_c and likewise for n_B; values of D are not calculated, since they are not needed in the subsequent analysis. (Thanks to Steen Christensen of the Technical University of Denmark for pointing out that the common bond vectors were reversed in direction!) The following three conditions must be met for a unit vector in a given plane, û_F or û_B respectively, that is also perpendicular to F_c-B_c:

where these equations are applicable to either plane. In graphical terms, these unit vectors appear as something like:

To simplify the algebra, the planes are  translated to pass through the origin by translating the atom F_c exactly to the origin, and translating the other three atoms with the same transformation:

This makes D = 0 for eq. 3 while retaining the relative locations of each atom. (Therefore, it is irrelevant whether eq. 1 is carried out before or after translation by eq. 5.) Solving the three eqs. 2 to 4 for the components of û gives:

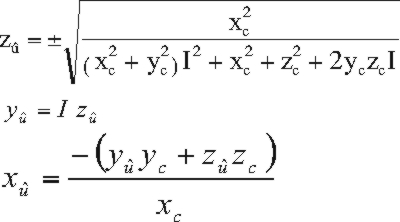           (6)

where I is given by:

I = (A z_c/x_c - C)  /  (B - A y_c/x_c)                                                            (7)

and (x_c, y_c, z_c) represents the component form of the vector F_c-B_c; as long as this is carried out after transformation by eq. 5, the simplification that D=0 will be valid. Note that eq. 6 has two roots. In order to ensure that the appropriate û is in the direction of F₁ or B₁, as in the above figure illustrating û_F and û_B, the desired unit vector is that set of coordinates which forms a smaller angle of form û_F-F_c-F1 or û_B-B_c-B1, respectively. The magnitude of the dihedral angle illustrated is then given by the angle between the two unit vectors, û_F and û_B. For the less geometrically inclined, a nice simple way to calculate this is:

which simplifies very nicely since both are unit vectors, and are therefore length (= norm symbol ||x||) 1, to

Finally, the sign of the dihedral angle must be determined:

Thanks to Dr. John W. Logan from Stanford for alerting me to the following method for sign calculation which answers my plea of "there must be a simpler way to do this"! (My original method employing rotation matrices is given below - but, the much more efficient method employs a single dot product.) This is based on an article by Bekker et al. in J. Comp. Chem. 16: 527 (1995), which forms Chapter 5 of H. Bekker's Ph.D. Dissteration available at RUG. Note that the above calculation is all based on a cross-product definition; a dot-product definition may also be derived - Dr. Logan tested this out and found it to be computationally slower than the cross-product definition. (See again Bekker's work for a comparison of the two definitions.)

If we consider the following projection looking down the bond F_c->B_c

we can make use of the angle α between n_B and bond vector (F_c-F₁). As you can see from the above diagram, any dihedral angle with a negative sign (as the shown angle is) will have angle α with a magnitude greater than 90°. Conversely, once bond vector (B_c-B₁) goes into the region of the plane shown above where it implies a postive dihedral, α will have a magnitude less than 90°. So, this means that we can go ahead and exploit the dot product: a dot product between n_B and bond vector (F_c-F₁) will be positive when |α| < 90° & negative when 90° < |α| <= 180°. So, you can get the sign of the dihedral by:
    sign = sign(n_B·(F_c-F₁))

Note: Although I haven't personally tested the above sign expression yet, David Lomelin from UCSF tells me that it indeed works. He was also nice enough to send the following correction: the criteria should be <= 180° (as now listed), rather than just < 180° as was originally listed!

Unfortunately (from the simplicity standpoint), the way that I came up with to do this determination consistently time after time requires a series of rotations. Here, the goal is to rotate F_c-B_c such that it is parallel to an axis; this allows direct comparison of the relative angles of each of the û vectors. First a rotation about z is carried out to bring F_c-B_c into the xy-plane using

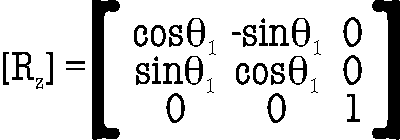               (10)

with

with the constraint that θ₁ in this case is determined such that rotation is carried out to the nearest z axis (i.e., if 180° > |α| > 90° then α = - (180° - α) with the necessary 360° subtraction if (180° - α) > 180°.) This rotation, and the subsequent one, are applied to F_c-B_c, û_F, and û_B. Second, the three vectors are rotated about the y-axis

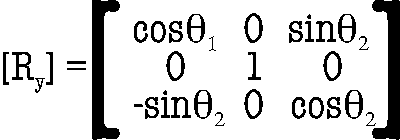                (12)

to bring the rotated F_c-B_c to the x-axis; here the angle between (F_c-B_c)’ and the positive x-axis is given by

Note: I use one ' to represent a vector or vector component with one rotation carried out or '' for the doubly rotated version. Each of the vectors û_F'' and û_B'' now have components only in the yz-plane since they were both defined as perpendicular to the F_c-B_c vector. The (relative) angle assumed by each is given by

for each vector. Comparison of the angle of rotation of û_F'' to û_B'' then readily provides the sign of the dihedral angle. Specifically, if û_F'' is rotated clockwise relative to û_B'' by less than 180° (as is the case illustrated in last of the Figures above) the dihedral angle will be positive; conversely, a counterclockwise rotation in such a relative frame is negative. Note that if (F_c-B_c)’’ lies along the -x-axis instead of the +x-axis the rotations will be reversed.

So, that's my method to calculate and assign correct signs to dihedral angles. This worked consistently for a dataset of somewhere in the ballpark of 180,000 residues, so I'm quite sure it is reliable. There may very well be a simpler way to do this, but I couldn't think of one or find one discussed. Please let me know if you have issues with this etc., find mistakes (this is transcribed from my thesis, which is transcribed from the original pencil and paper derivation - I've checked it fairly closely, though), or know of some super simple way to do the same thing!

Last updated: June 2, 2005.